Research
My research aims to exploit mathematical tools in stochastic analysis, e.g., diffusion-operator theory, stochastic calculus and rough path theory, to enhance the development and analysis of modern statistical machine learning and signal processing algorithms. This finds application in:- generative modeling
- inverse reinforcement learning
- algorithmic game theory
Below are a few representative projects, see my publications for a full list.
Efficient Neural SDE Training via Wiener–Space Cubature
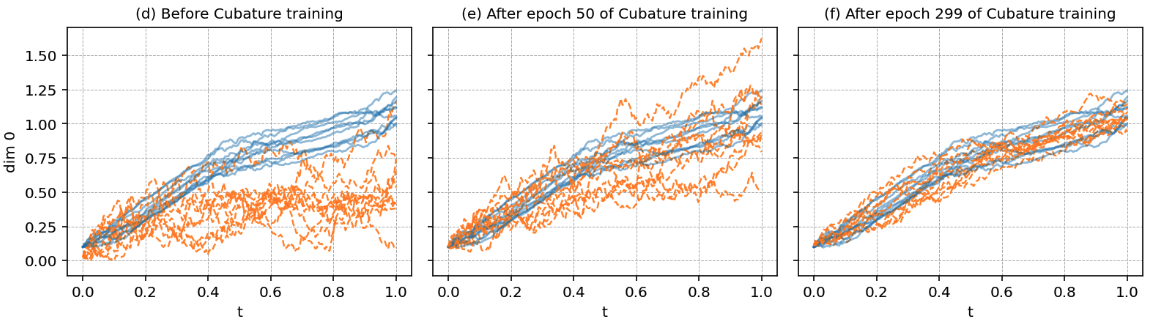
Neural stochastic differential equations (SDEs) parametrize SDE drift and diffusion vector fields as neural networks, serving as an emerging expressive framework for time-series generative modeling. They are trained by minimizing an expected loss functional over path space, capturing the discrepancy between induced sample paths and time-series data. We innovate on contemporary training pipelines by introducing a cubature-based loss evaluation that replaces Monte-Carlo path evaluation with a weighted sum of deterministic ODE solutions.
This is a fundamental paradigm shift, enabling ultra-efficient neural SDE training by bypassing Brownian path computations, exploiting memory-efficient parallel ODE solvers, and reducing the number of paths needed for a given accuracy. Specifically, we show that this method achieves O(n−1) convergence in path evaluations, outperforming naïve Monte Carlo (O(n−1/2)) and quasi–Monte Carlo (O((log n)/n)).
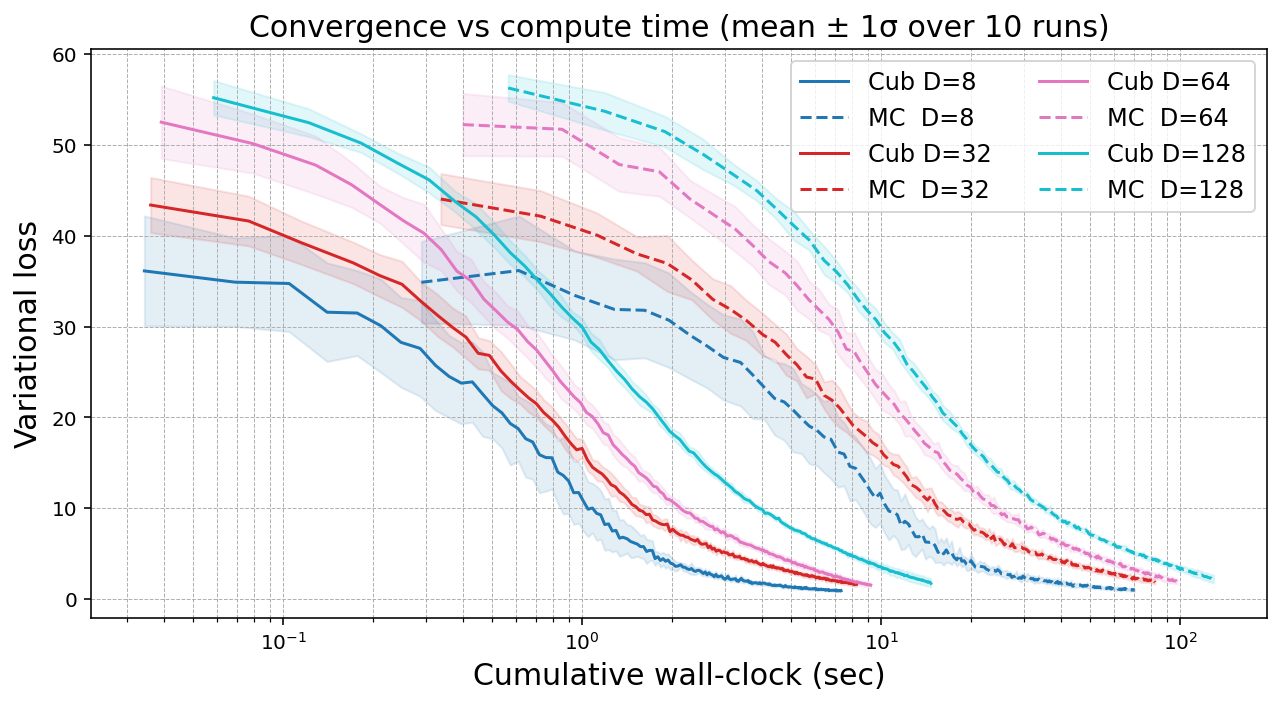
Mathematically, these guarantees are enabled by novel extensions of Wiener–space cubature guarantees to Lipschitz–nonlinear path functionals necessary for diffusion training, yielding rigorous error bounds for approximating expected objectives by deterministic ODE evaluations.
Efficient Neural SDE Training using Wiener-Space Cubature
arXiv:2502.12395, 2025 [pdf]
Passive Langevin Dynamics for Adaptive Inverse Reinforcement Learning

Suppose an agent enacts a stochastic optimization algorithm to minimize a cost function. By observing sequential noisy gradients from this process, how can we (an external observer) reconstruct this cost function in its entirety? This is a generalized transient-learning analog of inverse reinforcement learning (IRL), in which the reward function of a reinforcement learning agent is recovered by observing optimal policy evaluations.
We develop a passive stochastic gradient Langevin dynamics (PSGLD) algorithm which accomplishes this adaptive IRL objective, and provide sample complexity bounds for the cost function reconstruction accuracy, exploiting tools in the theory of Markov diffusion operators.
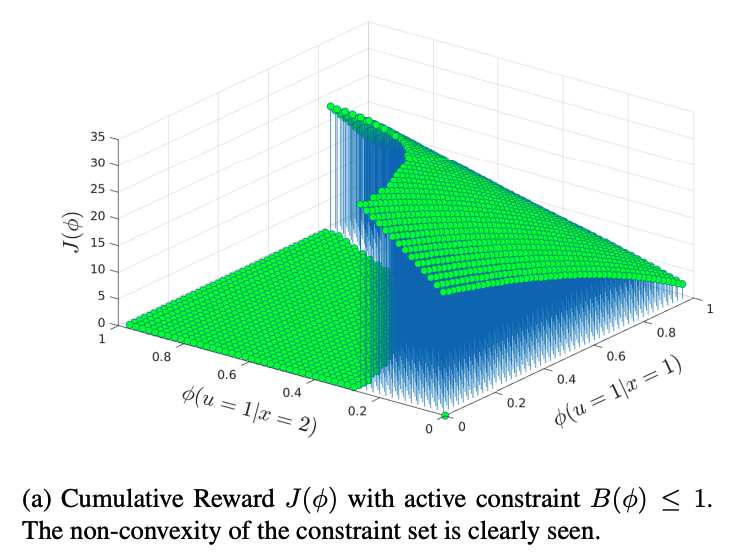
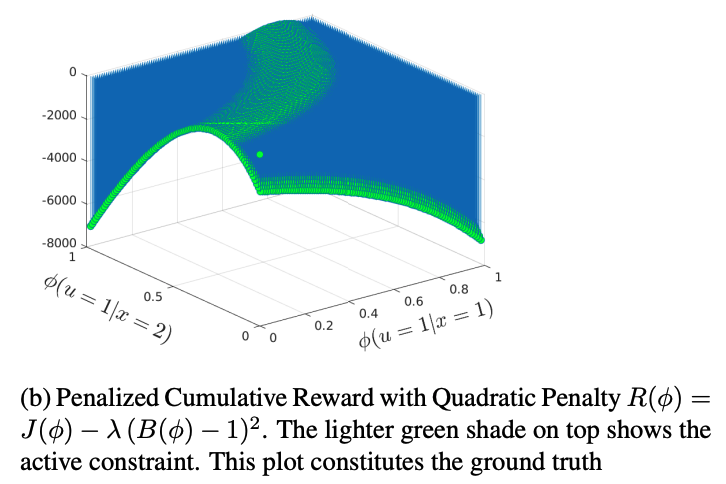

Finite-Sample Bounds for Adaptive Inverse Reinforcement Learning using Passive Langevin Dynamics
IEEE Transactions on Information Theory, 2025 [pdf]
Data-Driven Mechanism Design using Multi-Agent Revealed Preferences
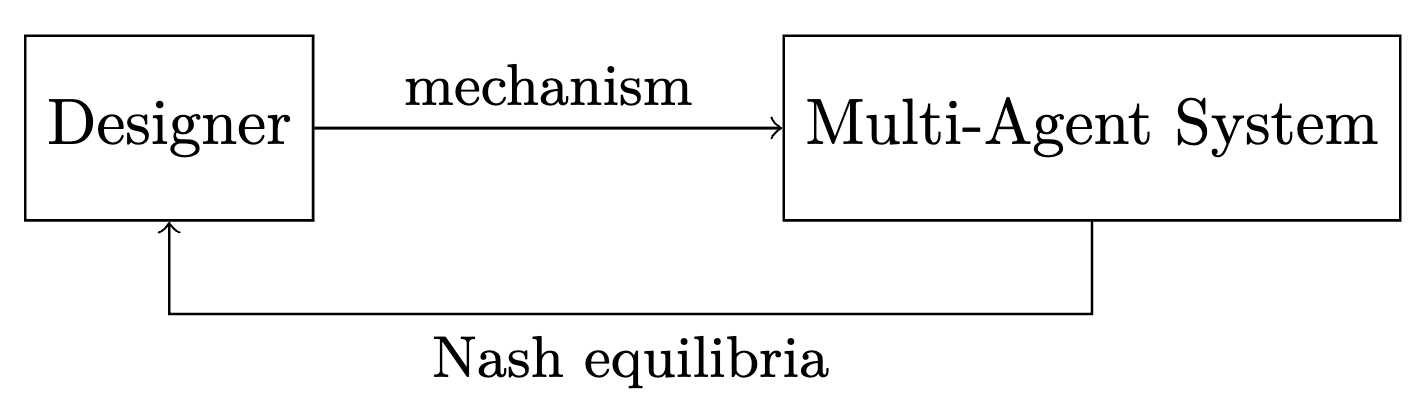
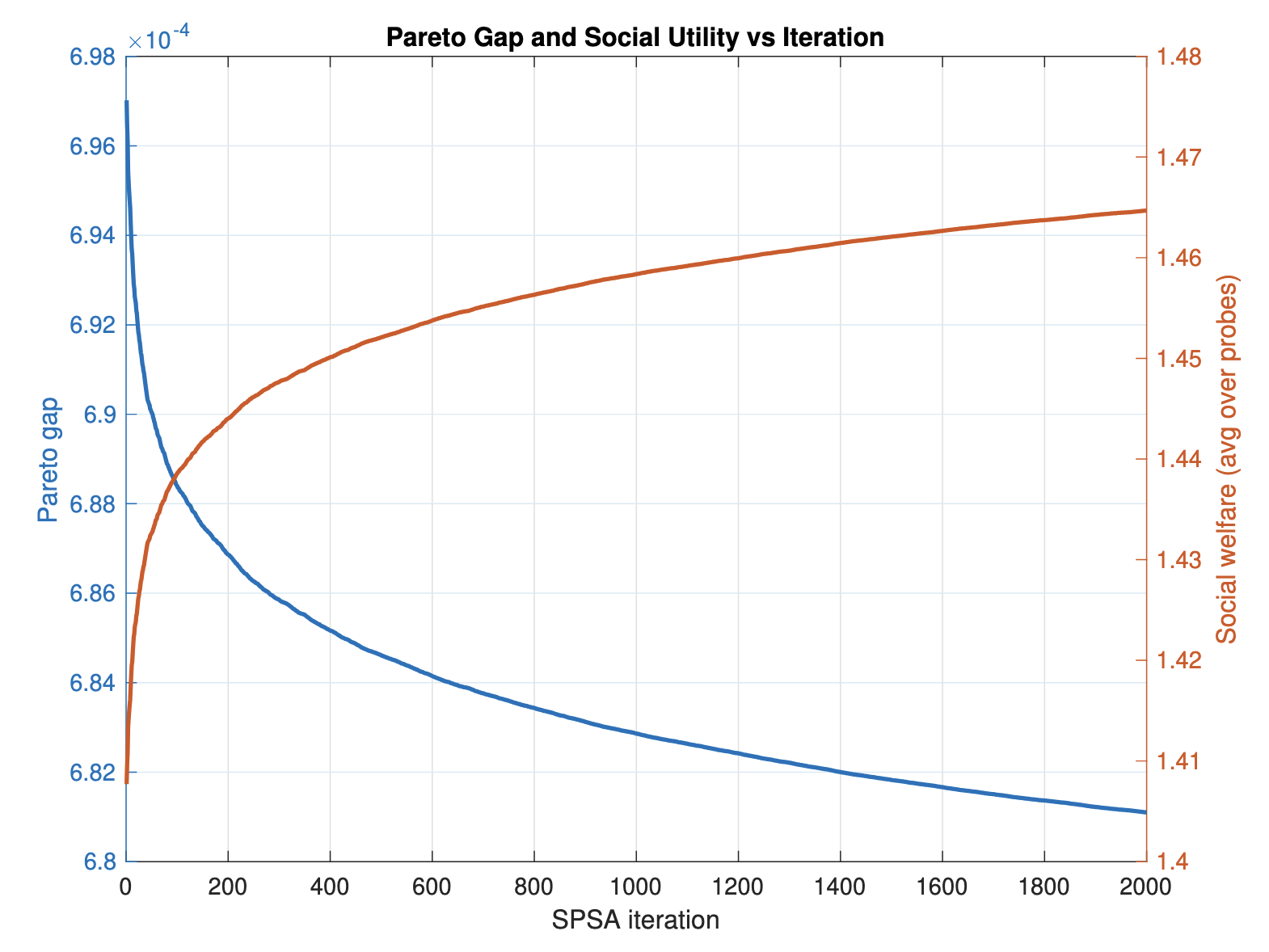
The stable behavior of strategically interacting multi-agent systems is captured by equilibria concepts such as Nash equilibria. However, non-cooperative strategic equilibria often degrade the performance (utility attained) of each agent in the system. A goal of mechanism design is to fashion the game structure (mapping from agent actions to outcomes) such that non-cooperative interactions lead to outcomes which maximize the performance (utility) of all agents.
We provide a novel algorithmic approach to accomplishing mechanism design adaptively, by iteratively interacting with the system and observing Nash equilibria. Our framework allows for mechanism design to be achieved even when the designer has no observation of the agent utilities. We exploit tools from microeconomic revealed preference theory.
Data-Driven Mechanism Design using Multi-Agent Revealed Preferences
arXiv:2404.15391, 2024
[pdf]